Решение упражнения номер 1104 – Геометрия 9 класс Атанасян Л.С.

1104

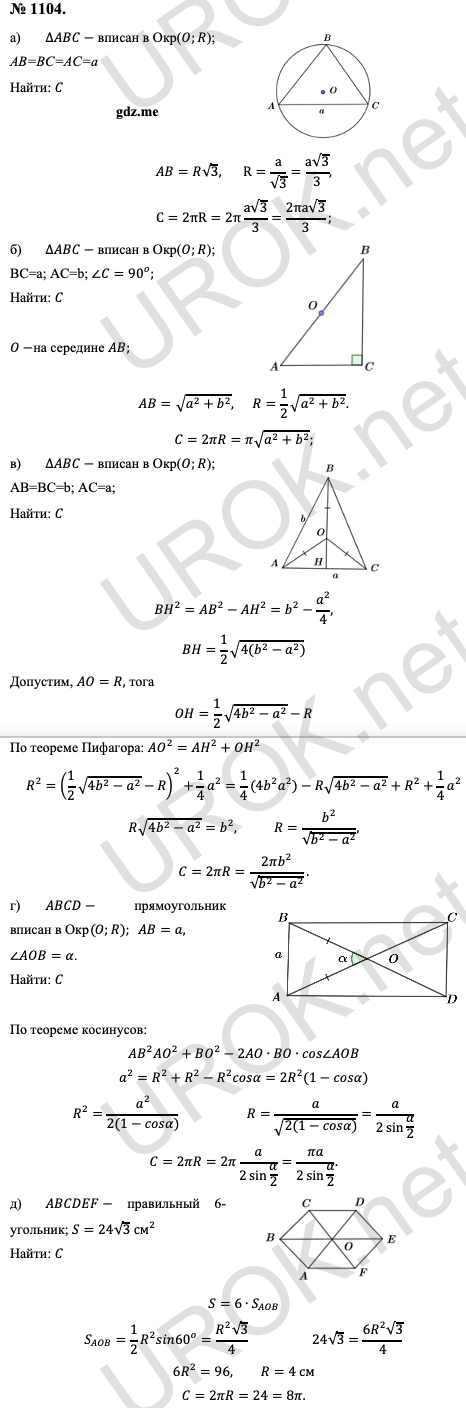
Найдите длину окружности, описанной около: а) правильного треугольника со стороной а; б) прямоугольного треугольника с катетами а и b; в) равнобедренного треугольника с основанием а и боковой стороной b; г) прямоугольника с меньшей стороной а и острым углом ос между диагоналями; д) правильного шестиугольника, площадь которого равна 24корень3 см2.

Ответ
Ответ с подробным решением задания Геометрия 9 класс Атанасян: 1104. Дано: ∆ABC- вписан в Окр(O.R). AB=BC=AC=a Найти: C AB=R√3, R=a/√3=(a√3)/3, C=2πR=2π (a√3)/3=(2πa√3)/3. Дано: ∆ABC- вписан в Окр(O.R). BC=a. AC=b. ∠C=90^o. Найти: C Решение: O-на середине AB. AB=√(a^2+b^2 ), R=1/2 √(a^2+b^2 ). C=2πR=π√(a^2+b^2 ). Дано: ∆ABC- вписан в Окр(O.R). AB=BC=b. AC=a. Найти: C Решение: BH^2=AB^2-AH^2=b^2-a^2/4, BH=1/2 √(4(b^2-a^2 ) ) Пусть AO=R, тога OH=1/2 √(4b^2-a^2 )-R По теореме Пифагора: AO^2=AH^2+OH^2 R^2=(1/2 √(4b^2-a^2 )-R)^2+1/4 a^2=1/4 (4b^2 a^2 )-R√(4b^2-a^2 )+R^2+1/4 a^2 R√(4b^2-a^2 )=b^2, R=b^2/√(b^2-a^2 ), C=2πR=(2πb^2)/√(b^2-a^2 ). Дано: ABCD- прямоугольник вписан в Окр(O.R). AB=a, ∠AOB=α. Найти: C Решение: По теореме косинусов: AB^2 AO^2+BO^2-2AO∙BO∙cos∠AOB a^2=R^2+R^2-R^2 cosα=2R^2 (1-cosα) R^2=a^2/(2(1-cosα)) R=a/√(2(1-cosα))=a/(2 sin〖α/2〗 ) C=2πR=2π a/(2 sin〖α/2〗 )=πa/(2 sin〖α/2〗 ). Дано: ABCDEF- правильный 6- угольник. S=24√3 см^2 Найти: C Решение: S=6∙S_AOB S_AOB=1/2 R^2 sin60^o=(R^2 √3)/4 24√3=(〖6R〗^2 √3)/4 〖6R〗^2=96, R=4 см C=2πR=24=8π.